Обучение нейронных сетей
Процесс настройки весов для минимизации ошибки и достижения высокой точности предсказаний
Процесс обучения
Обучение нейронной сети — это итеративный процесс настройки весов связей между нейронами для минимизации ошибки предсказания на обучающих данных.
Процесс обучения начинается с инициализации весов сети случайными значениями. Затем сеть обрабатывает обучающие данные, вычисляет выходные значения и сравнивает их с ожидаемыми результатами. Разница между предсказанными и фактическими значениями называется ошибкой или функцией потерь.
Цель обучения — найти такие значения весов, которые минимизируют функцию потерь на обучающих данных. Это достигается путем многократного прохода по обучающим данным и корректировки весов в направлении, которое уменьшает ошибку. Процесс продолжается до тех пор, пока ошибка не достигнет приемлемого уровня или не перестанет уменьшаться.
Обучение может быть контролируемым, когда сеть обучается на размеченных данных с известными правильными ответами, или неконтролируемым, когда сеть находит закономерности в данных без явных меток. Также существует обучение с подкреплением, где сеть учится на основе взаимодействия со средой и получает обратную связь в виде наград или штрафов.
Обратное распространение ошибки
Алгоритм обратного распространения
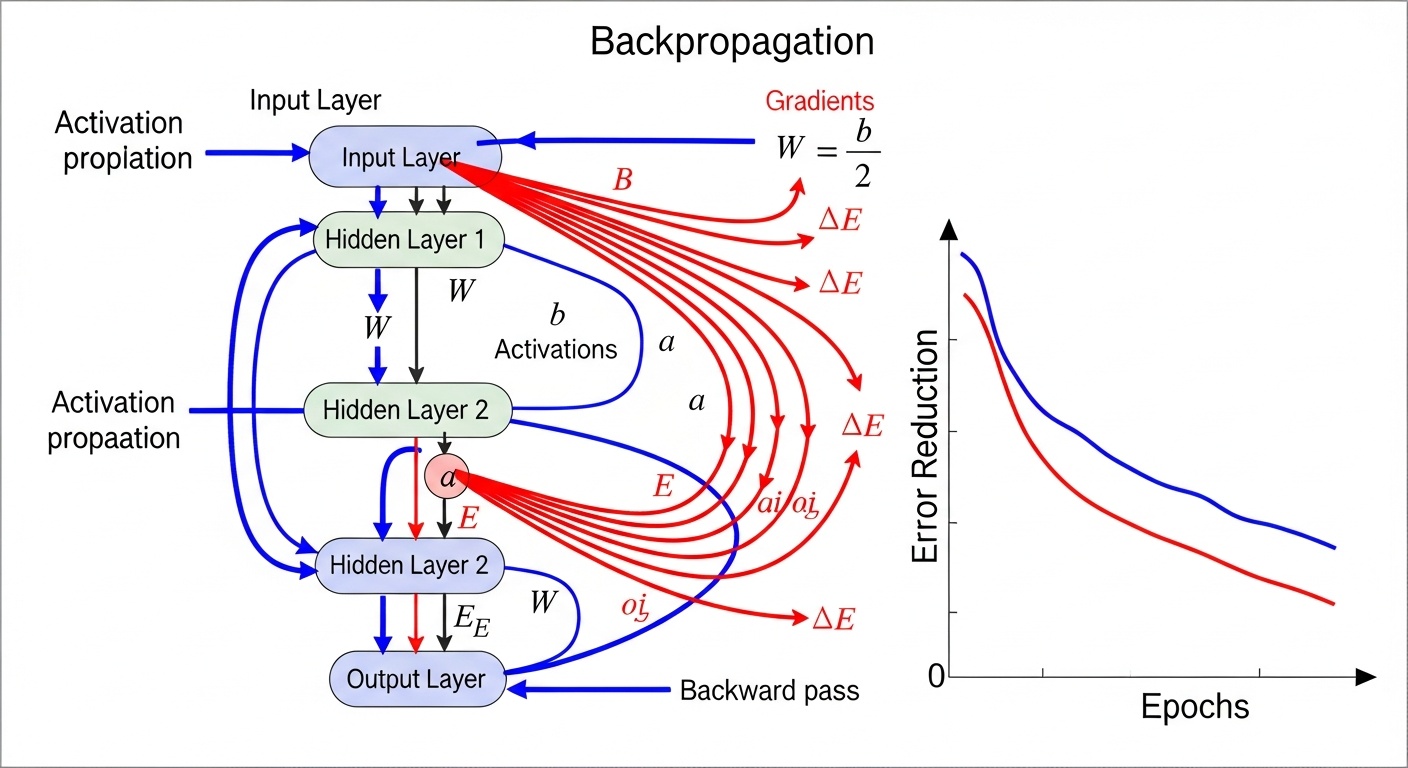
Обратное распространение ошибки (backpropagation) — это основной алгоритм обучения многослойных нейронных сетей. Он работает в два этапа: прямой проход и обратный проход.
В прямом проходе входные данные проходят через сеть от входного слоя к выходному, и на каждом слое вычисляются активации нейронов. Выходные значения сети сравниваются с ожидаемыми результатами, и вычисляется ошибка.
В обратном проходе ошибка распространяется назад через сеть, и для каждого веса вычисляется градиент функции потерь. Эти градиенты показывают, как нужно изменить веса, чтобы уменьшить ошибку. Веса обновляются в направлении, противоположном градиенту, с использованием алгоритма оптимизации, такого как градиентный спуск.
Оптимизация
Алгоритмы оптимизации определяют, как именно обновляются веса сети на основе вычисленных градиентов.
Градиентный спуск
Стандартный градиентный спуск обновляет все веса одновременно после обработки всего обучающего набора данных. Это может быть медленным для больших наборов данных, но обеспечивает стабильное обучение.
Основной недостаток — необходимость хранить весь обучающий набор в памяти и вычислять градиенты для всех примеров перед обновлением весов. Это делает стандартный градиентный спуск непрактичным для очень больших наборов данных.
Стохастический градиентный спуск
Стохастический градиентный спуск (SGD) обновляет веса после обработки каждого отдельного примера. Это делает обучение быстрее и позволяет обрабатывать данные по мере их поступления.
SGD может быть более шумным, чем стандартный градиентный спуск, но часто сходится быстрее и может избежать локальных минимумов. Современные варианты SGD, такие как Adam и RMSprop, адаптивно настраивают скорость обучения для каждого параметра.
Адаптивные методы
Адаптивные алгоритмы оптимизации, такие как Adam, RMSprop и AdaGrad, автоматически настраивают скорость обучения для каждого параметра. Это делает обучение более эффективным и устойчивым к выбору гиперпараметров.
Эти методы отслеживают историю градиентов и используют эту информацию для адаптации скорости обучения. Adam, в частности, комбинирует преимущества адаптивного градиентного алгоритма и импульса, что делает его одним из самых популярных методов оптимизации.
Регуляризация
Регуляризация — это набор техник, используемых для предотвращения переобучения нейронных сетей. Переобучение происходит, когда сеть слишком хорошо запоминает обучающие данные и плохо обобщается на новые данные.
Dropout — одна из самых популярных техник регуляризации. Во время обучения случайно выбранные нейроны временно "отключаются" с определенной вероятностью. Это заставляет сеть не полагаться слишком сильно на отдельные нейроны и учиться более устойчивым представлениям.
L1 и L2 регуляризация добавляют штраф к функции потерь за большие значения весов. L2 регуляризация (также называемая weight decay) штрафует квадраты весов, что приводит к более плавному распределению весов. L1 регуляризация штрафует абсолютные значения весов, что может привести к обнулению некоторых весов и созданию разреженных моделей.