Искусственные нейроны
Основная единица нейронных сетей и ключ к пониманию машинного обучения
Что такое искусственный нейрон
Искусственный нейрон — это математическая модель биологического нейрона, которая является фундаментальным строительным блоком нейронных сетей.
Искусственный нейрон, также называемый узлом или единицей обработки, представляет собой вычислительную единицу, которая получает один или несколько входных сигналов, обрабатывает их и производит выходной сигнал. Концепция искусственного нейрона была вдохновлена работой биологических нейронов в мозге, которые получают сигналы через дендриты, обрабатывают их в теле клетки и передают результаты через аксон.
В искусственных нейронных сетях каждый нейрон соединен с множеством других нейронов через взвешенные связи. Эти веса определяют силу влияния одного нейрона на другой. Когда нейрон получает входные данные, он вычисляет взвешенную сумму всех входов, добавляет смещение (bias) и применяет функцию активации для получения выходного значения.
Математически это можно выразить как: выход = активация(Σ(вход × вес) + смещение). Эта простая формула лежит в основе всех сложных вычислений, которые выполняют современные нейронные сети, от распознавания изображений до генерации текста.
Структура нейрона
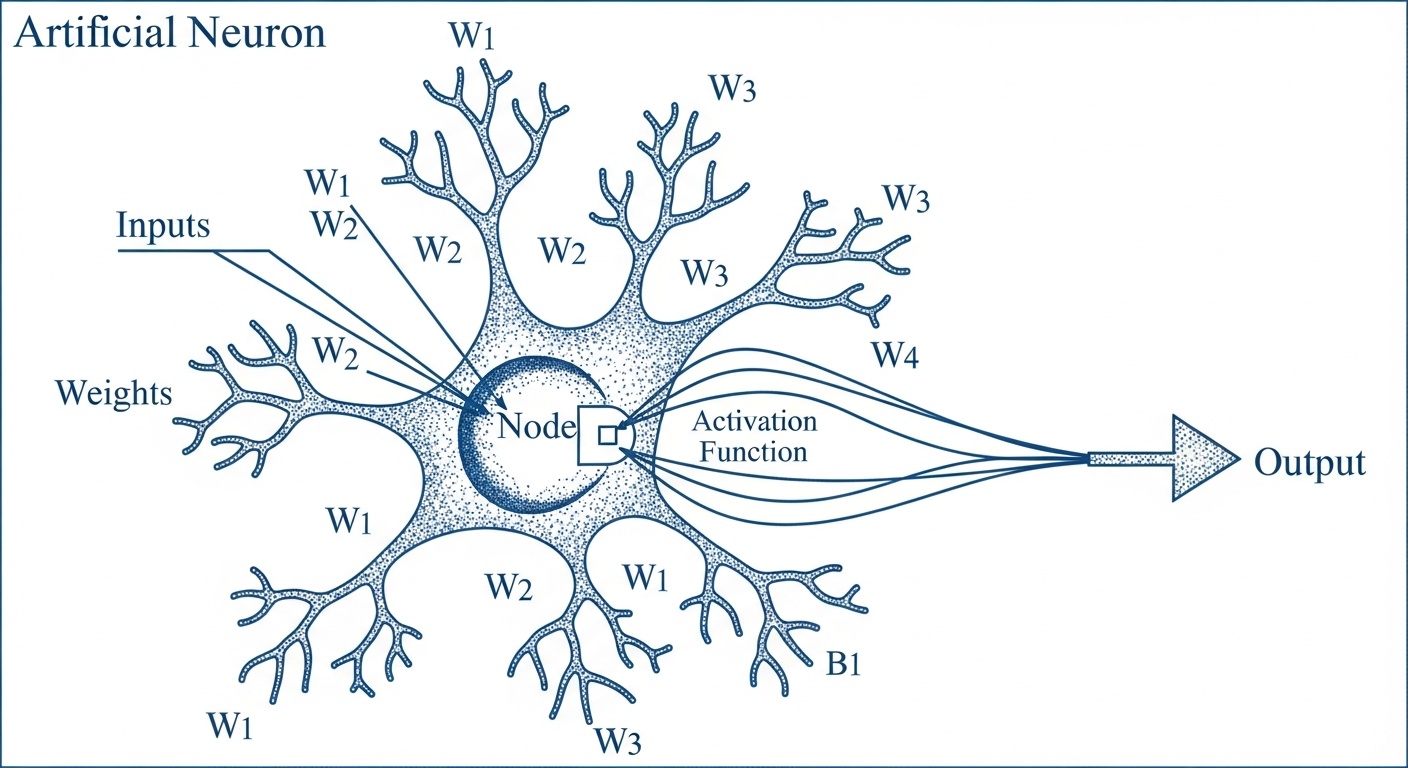
Основные компоненты
Каждый искусственный нейрон состоит из нескольких ключевых компонентов. Входные связи (синапсы) передают сигналы от других нейронов, каждый сигнал умножается на соответствующий вес связи. Эти взвешенные входы суммируются вместе с добавлением смещения.
Сумматор объединяет все взвешенные входы и смещение в одно значение. Это значение затем передается в функцию активации, которая определяет, будет ли нейрон активирован и с какой силой. Функция активации вводит нелинейность в систему, что позволяет нейронным сетям моделировать сложные нелинейные зависимости.
Выходной сигнал нейрона затем передается другим нейронам в сети через выходные связи. Сила этих связей определяется весами, которые настраиваются в процессе обучения сети для минимизации ошибки предсказания.
Функции активации
Функция активации определяет выход нейрона на основе взвешенной суммы входов и играет критическую роль в способности сети изучать сложные закономерности.
ReLU
Rectified Linear Unit (ReLU) — одна из самых популярных функций активации в современных нейронных сетях. Она возвращает входное значение, если оно положительное, и ноль в противном случае: f(x) = max(0, x).
ReLU проста в вычислении и помогает решить проблему затухающих градиентов, которая возникает в глубоких сетях с сигмоидными функциями. Однако ReLU может страдать от проблемы "мертвых нейронов", когда нейрон всегда выдает ноль и перестает обучаться.
Сигмоида
Сигмоидальная функция активации преобразует входное значение в диапазон от 0 до 1: f(x) = 1 / (1 + e^(-x)). Эта функция плавная и дифференцируемая, что делает ее полезной для задач, где требуется вероятностная интерпретация выхода.
Сигмоида широко использовалась в ранних нейронных сетях, но в глубоких сетях она может вызывать проблемы с затухающими градиентами. Тем не менее, она все еще используется в выходных слоях для задач бинарной классификации.
Гиперболический тангенс
Гиперболический тангенс (tanh) преобразует входное значение в диапазон от -1 до 1: f(x) = tanh(x). Эта функция симметрична относительно нуля, что может быть полезно для центрированных данных.
Tanh часто работает лучше, чем сигмоида, в скрытых слоях, так как ее выходы центрированы вокруг нуля. Однако она все еще может страдать от проблем с затухающими градиентами в очень глубоких сетях.
Типы нейронов
В зависимости от их положения в сети и выполняемых функций, нейроны можно классифицировать на несколько типов. Входные нейроны получают данные из внешнего источника и передают их в сеть без какой-либо обработки. Они служат интерфейсом между внешним миром и нейронной сетью.
Скрытые нейроны находятся между входным и выходным слоями и выполняют основную вычислительную работу сети. Они извлекают признаки из входных данных и комбинируют их для создания более абстрактных представлений. Количество и структура скрытых слоев определяют способность сети изучать сложные закономерности.
Выходные нейроны производят окончательный результат работы сети. В задачах классификации они обычно используют функцию активации softmax, которая преобразует выходы в вероятности принадлежности к каждому классу. В задачах регрессии выходные нейроны могут использовать линейную активацию или вообще не иметь функции активации для производства числовых значений.